GNSS Local Transformation
Overview
Due to a variety of reasons, it may be necessary to adjust position coordinates for distortions which can include scale, rotation, translation in northing and translation in easting. The flexibility of FieldGenius's local transformation utility allows it to be used for a variety of applications and applied to positions derived from GNSS or terrestrial observations. For GNSS applications there are two possible reasons for the need of a transformation:
-
Translating from Local System to Plan System
GNSS receivers by default generate geodetic coordinates (latitude, longitude and ellipsoidal height) and the process of converting to Cartesian coordinates (northing, easting and orthometric height) or local system is done with existing well defined map projection systems such as Universal Transverse Mercator (UTM) or the State Plane Coordinate System (SPCS). Selection of the map projection in FieldGenius is done within the Datum page of the GNSS Configuration and a local zone is selected to minimize scale and meridian convergence distortion. Most land, boundary or property surveys are unique with regards to their generalized plane and coordinate origin for each Project. The coordinate system for these surveys is often referred to as a plan system with coordinate magnitudes being kept small for ease of recording and calculations. The majority of Projects can suffice with a simple translation in northing and easting to produce plan system coordinates from GNSS determined local system coordinates. The translation is easily determined by comparing a plan system coordinate and a local system coordinated for a single point. -
Consideration for Scale and Rotation
Projects with larger extents need to take into consideration the curvature of the earth's surface which can be handled by the application of scale and rotation transformations plus the previously mentioned translations. In the case of mixing GNSS observations and terrestrial observations it does become important to apply a transformation, especially in scale, due to the fact that there is a difference in distance between positions measured on the ellipsoid and the terrain surface. As seen in Figure 1, coordinates derived from GNSS are always referenced to the surface of the ellipsoid as per the application of map projections. When the two points on the ellipsoid are projected upwards along the ellipsoid normals onto the earth's surface, they diverge, and a terrestrial distance observed between the points will be greater than the computed distance of the same two points on the ellipsoid. The effects of this zenith divergence becomes more evident as distance between the two points becomes greater and for larger terrain heights above the ellipsoidal surface.
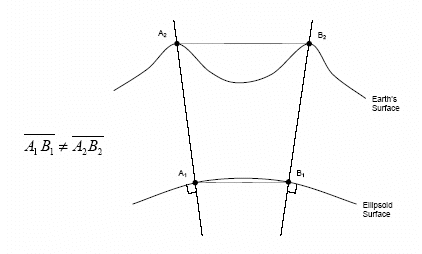
Figure 1. Divergence of Ellipsoid Normals.
Transformation Concepts
In order for the transformation parameters to be resolved, a sufficient number of control points are required with coordinates in both the plan system and local system. The determination of a four parameter transformation (two translations, scale and rotation) on a horizontal plane requires at minimum two physical points with each having two sets of corresponding coordinates as illustrated in Figure 2. Points A1 and B1 exist in what is termed the local system and are transformed into the plan system points of A2 and B2. The use of more coordinate observations will provide redundancy and the means to identify outliers for elimination. Solving for over constrained parameters is done with the application of least squares to provide the most rigorous minimization of residuals. Once transformation parameters have been resolved, newly observed or existing coordinates can easily be converted to the plan coordinate system.

Figure 2. Horizontal Four Parameter Transformation.
The selection of control points for determining the transformation parameters are critical in reducing a colinearity condition along a particular axis. Colinearity will present itself if the control points are concentrated in a linear fashion as shown in Figure 3 (Poor Design) and thus weaken the parameters in a perpendicular direction. Control points should extend to the corners of the Project boundary and be extended with equal distances in both horizontal directions.
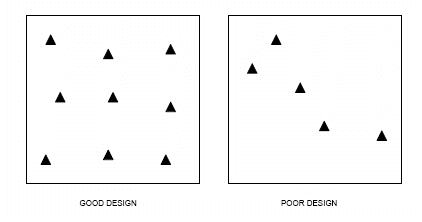
Figure 3. Transformation Control Design.
Vertical Transformation
The vertical transformation function of FieldGenius operates independently of the horizontal transformation. A sloped plane is calculated from the residuals of the constrained point pairs to determine a vertical bias, slope in X and slope in Y. To determine a vertical bias at least one point pair must be constrained and for all three parameters to be determined at least three point pairs must be constrained.
The use of the vertical transformation function should be restricted to cases where a geoid model is not available or there is a known problem with an existing geoid model.